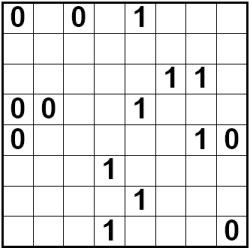
Binaire Sudoku's / Binary Sudoku
Solutions algorithm

Content
1. Explanation
3. Three or more blanks patterns with mimum number of '0' (or '1')
4. Three or more blanks patterns with maximum number of '0' (or '1')
5. Three or more blanks patterns (all)
1. Explanations
Definitions: x and y are blanco's, that means they can be either '0' or '1'.
Generals rules for dubbles 00, 11, 0x0, 1y1, missing '0' or missing '1', uneuqal rows or unequal columns are know. Additions patterns and solutions/algorithms are given below.
* Notes
1). Solution given below are mostly if one symbol '0' (or one symbol '1') is left. The pattern given below needs that single symbol '0' (respectively '1'), with the consequence that all other blanks, not included in the pattern given, should be '1' (respectively '0').
2). If, in general, the pattern is N times present with N symbols '0' (or N symbols '1'), the consequences are that all other blanks should be '1' (respectively '0')
Patttern 0□□/ 1□□
The pattern 0xx needs one symbol '1'. See also notes 1 and 2 *)
The pattern 1xx needs one symbol '0'. See also notes 1 and 2 *)
Patttern □0□ / □1□
The pattern x0x needs one symbol '1'. See also notes 1 and 2 *)
The pattern x1x needs one symbol '0'. See also notes 1 and 2 *)
3. Three or more blanks patterns with mimum number of '0' (or '1')
1. The solutions below are for the minimum numbers (Nmin) of symbols '0' in the patterns shown. With a repetition of 3 blanks there are unique solutions.
These unique patterns are given in the general formula N*(xxx)+y.
E.g. N*(110)+11 with N=3, the blanks will give the pattern 11011011011 for 11 blanks, with at least 4 symbols of '0'.
This will be possible in the pattern 0xxx xxx xxx xx0, see below.
In other cases there are no unique solutions, but there is always a minimum number Nmin of '0' in the pattern concerned.
The general formula for Nmin is integer((#blanks+X)/3), with X between -2 and +2. Eg. 4 blanks in the pattern 0xxxx0 needs at least int(4/3)=1 symbol of '0'.
2. If the remaining number of symbols '0' is equal to the minimum number of symbols for the patterns below, all other remaning blanks will be '1'.
E.g. On a row there are found a pattern 0x...x0 which needs at least 2 symbols '0' and an other pattern 1x...., which needs at least one symbol '0' and there are still 3 symbols '0' lacking on the row, that means both patterns needs these 3 symbols '0'. But that means also that all other blanks, in other patterns, must be '1'.
3. The same holds for the symbol '1'. Exchange '0' and '1' in the solutions below.
Patttern 0□...□0
The minimum of symbols '0' Nmin= integer(#blanks/3) . There are unique solutions for the blanks with the format: N*(110)+11, if the number of blanks= 3N+2.
Patttern 0□...□1
The minimum of symbols '0' Nmin= integer((#blanks+1)/3) . There are unique solutions for the blanks with the format: N*(110)+1, if the number of blanks = 3N+1.
Patttern 1□...□1
The minimum of symbols '0' Nmin= integer((#blanks+2)/3) . There are unique solutions for the blanks with the format: N*(101), if the number of blanks = 3N.
Patttern 1□...□
The minimum of symbols '0' Nmin= integer((#blanks+1)/3) . There are unique solutions for the blanks with the format: N*(101)+1, if the number of blanks = 3N+1.
Patttern 0□...□
The minimum of symbols '0' Nmin= integer(#blanks/3) . There are unique solutions for the blanks with the format: N*(110)+11, if the number of blanks = 3N+2.
Table 1. The fomula for the minimum of number of symbols '0' and in special cases the unique solution.
| first and second unique pattern | minimum # of '0' | |||||
| Pattern | Formula | blanks | Formula | #Blanks | Formula | # |
| 0x…x0 | N(110)11 | 11011 | 3N+2 | 5 | int(#B/3) | 1 |
| 11011011 | 8 | 2 | ||||
| 0x…x1 | N(110)1 | 1101 | 3N+1 | 4 | int((#B+1)/3) | 1 |
| 1101101 | 7 | 2 | ||||
| 1x…x1 | N(101) | 101 | 3N | 3 | int((#B+2)/3) | 1 |
| 101101 | 6 | 2 | ||||
| 1x….. | N(101)1 | 1011 | 3N+1 | 4 | int((#B+1)/3) | 1 |
| 1011011 | 7 | 2 | ||||
| 0x….. | N(110)11 | 11011 | 3N+2 | 5 | int(#B/3) | 1 |
| 11011011 | 8 | 2 | ||||
4. The general formula for the unique patterns is: N(x)y with x=110 if any '0' is around the pattern concerned,
else x=101 if only '1' is around the pattern. With y= 0, 1 or 2 symbols of '1'. y=(2- the number of '1' around the pattern).
5. The number of blanks in the unique pattern is 3N+y, with y the same as above, y=(2- the number of '1' around the pattern).
Table 2. Unique solutions for a minimum of number of symbols '0' up to 8.
| minimum | P a t t e r n | ||
| #Blanks | # of '0' | from | to |
| 3 | 1 | 1xxx1 | 11011 |
| 4 | 1 | 1xxxx | 11011 |
| 4 | 1 | 0xxxx1 | 011011 |
| 5 | 1 | 0xxxxx | 011011 |
| 5 | 1 | 0xxxxx0 | 0110110 |
| 6 | 2 | 1xxxxxx1 | 11011011 |
| 7 | 2 | 1xxxxxxx | 11011011 |
| 8 | 2 | 0xxxxxxxx | 011011011 |
| 8 | 2 | 0xxxxxxxx0 | 0110110110 |
Table 3. The minimum number of symbols '0' = integer((#Blanks+B0)/3)
| P A T T E R N | |||||
| 0x…x0 | 0x…x1 | 1x…x1 | 1x….. | 0x….. | |
| #Blanks/B0 | 0 | 1 | 2 | 1 | 0 |
| 3 | 1 | 1 | 1* | 1 | 1 |
| 4 | 1 | 1* | 2 | 1* | 1 |
| 5 | 1* | 2 | 2 | 2 | 1* |
| 6 | 2 | 2 | 2* | 2 | 2 |
| 7 | 2 | 2* | 3 | 2* | 2 |
| 8 | 2* | 3 | 3 | 3 | 2* |
*= unique patterns, see table 2.
6. It seems that B0 is equal to the number of symbols '1' around the pattern concerned (=y as gieven in point 4 and 5).
4. Three or more blanks patterns with maximum number of '0' (or '1')
Perhaps more interesting is the maximum number of symbols '0' in a particluar pattern.
Patttern 0□...□0
The maximum of symbols '0' Nmax= integer((#blanks+1)/3)+integer(#blanks/3) . There are unique solutions for the blanks with the format: N*(010), if the number of blanks= 2N.
Patttern 0□...□1
The maximum of symbols '0' Nmax= integer(#blanks/3)+integer((#blanks-1)/3) +1. There are unique solutions for the blanks with the format: N*(010)+0, if the number of blanks = 2N+1.
Patttern 1□...□1
The maximum of symbols '0' Nmax= integer((#blanks+2)/3)+integer((#blanks+1)/3). There are unique solutions for the blanks with the format: N*(001)+00, if the number of blanks = 2(N+1) with N=1,2,3...
Patttern 1□...□
The maximum of symbols '0' Nmax= integer(#blanks/3)+integer((#blanks-1)/3)+1.
- There are unique solutions for the blanks with the format: N*(001)+0, if the number of blanks = 2N+1 with N=1,2...
- There are unique solutions for the blanks with the format: N*(001)+00, if the number of blanks = 2N+2 with N=1,2 ,3...
- There are 2 solutions for the blanks with the format: N*(001)+10xx or N*(001)+10xx, if the number of blanks = 3N+2 with N=0,1,2...and with xx= 01 or 10
Patttern 0□...□
The maximum of symbols '0' Nmax= integer(#blanks/3)+integer((#blanks-1)/3)+1.
- There are unique solutions for the blanks with the format: N*(010), if the number of blanks = 2N with N=1,2...
- There are unique solutions for the blanks with the format: N*(020)+0, if the number of blanks = 2N+1 with N=1,2 ,3...
- There are 2 solutions for the blanks with the format: N*(010)+xx or N*(001)+xx, if the number of blanks = 2N+1 with N=0,1,2... and with xx= 01 or 10
7. The same holds for the symbol '1'. Exchange '0' and '1' in the solutions above.
| first and second unique pattern | maximum # of '0' | |||||
| Pattern | Formula | blanks | Formula | #Blanks | Formula | # |
| 0x…x0 | N(110)11 | 010 | 2N | 3 | int((B+1)/3)+int(B/3) | 1 |
| 010010 | 6 | 2 | ||||
| 0x…x1 | N(110)1 | 0100 | 2N+1 | 4 | int(B/3)+int((B-1)/3)+1 | 1 |
| 0100100 | 7 | 2 | ||||
| 1x…x1 | N(101) | 00100 | 2(N+1) | 5 | int((B+2)/3)+int((B+1)/3) | 1 |
| 00100100 | 8 | 2 | ||||
| 1x….. | N(001)0 | 0010 | 2N+1 | 4 | int((B+1)/3)+int((B-1)/3)+1 | 1 |
| 0010010 | 7 | 2 | ||||
| 1x….. | N(001)0yy | 0yy | 2N+2 | 3 | int((B+1)/3)+int((B-1)/3)+1 | 0 |
| 0010yy | 6 | 1 | ||||
| 1x….. | N(001)00 | 00100 | 2N+2 | 5 | int((B+1)/3)+int((B-1)/3)+1 | 1 |
| 00100100 | 8 | 2 | ||||
| 0x….. | N(010) | 010 | 2N | 3 | int(B/3)+int((B-1)/3)+1 | 1 |
| 010010 | 6 | 2 | ||||
| 0x….. | N(010)yy | 010yy | 2N+1 | 5 | int(B/3)+int((B-1)/3)+1 | 1 |
| 010010yy | 8 | 2 | ||||
| 0x….. | N(010)0 | 0100 | 2N+1 | 4 | int(B/3)+int((B-1)/3)+1 | 1 |
| 0100100 | 7 | 2 | ||||
| yy is either 01 or 10 | ||||||
| maximum | P a t t e r n | ||
| #Blanks | # of '0' | from | to |
| 3 | 2 | 0xxx0 | 00100 |
| 3 | 2 | 1xxx | 10yy |
| 3 | 2 | 0xxx | 00yy |
| 4 | 3 | 0xxx1 | 001001 |
| 4 | 3 | 1xxx | 10010 |
| 4 | 3 | 0xxx | 00100 |
| 5 | 4 | 1xxx1 | 1001001 |
| 5 | 4 | 1xxx | 100100 |
| 5 | 3 | 0xxx | 1100yy |
| 6 | 4 | 0xxx0 | 00100100 |
| 6 | 4 | 1xxx | 10010yy |
| 6 | 4 | 0xxx | 0010010 |
| 7 | 5 | 0xxx1 | 00100100 |
| 7 | 5 | 1xxx | 10010010 |
| 7 | 5 | 0xx | 00100100 |
| 8 | 6 | 1xxx1 | 1001001001 |
| 8 | 6 | 1xxx | 100100100 |
| 8 | 5 | 0xxx | 0010010yy |
| yy is either 01 or 10 | |||
| P A T T E R N | |||||
| 0x…x0 | 0x…x1 | 1x…x1 | 1x….. | 0x….. | |
| B0 | +1 | 0 | 2 | +1 | 0 |
| B1 | 0 | -1 | -1 | -1 | -1 |
| B2 | 0 | +1 | +1 | +1 | +1 |
| 3 | 2* | 2 | 2 | 2** | 2* |
| 4 | 2 | 3* | 3 | 3* | 3* |
| 5 | 3 | 3 | 4* | 4* | 3** |
| 6 | 4* | 4 | 4 | 4** | 4* |
| 7 | 4 | 5* | 5 | 5* | 5* |
| 8 | 5 | 5 | 6* | 6* | 5** |
| max # of '0: int((B+B0)/3)+int(B+B1)/3)+B2 with B=# blanks and pattern dependent constants B0, B1 and B2 | |||||
| *= unique pattern | |||||
| **= two solutions yy with yy= 01 or 10 |
|||||
5. Three or more blanks patterns (all)
Tabel: Sort on # of blanks
| # of '0' | # of '1' | ||||||
| min | min | P a t t e r n | |||||
| #Blanks | max | max | from | to | |||
| 3 | 2 | 1 | 0xxx0 | 00100 | |||
| 3 | - | - | 0xxx1 | - | |||
| 3 | 1 | 2 | 1xxx1 | 11011 | |||
| 3 | 2 | - | 1xxx | 10yy | |||
| 3 | - | 2 | 1xxx | 1101 | |||
| 3 | 2 | - | 0xxx | 00yy | |||
| 3 | - | 2 | 0xxx | 0010 | |||
| 4 | - | - | 0xxxx0 | - | |||
| 4 | 3 | 1 | 0xxxx1 | 001001 | |||
| 4 | 1 | 3 | 0xxxx1 | 011011 | |||
| 4 | - | - | 1xxxx1 | - | |||
| 4 | 1 | 3 | 1xxxx | 11011 | |||
| 4 | 3 | - | 1xxxx | 10010 | |||
| 4 | 3 | 1 | 0xxxx | 00100 | |||
| 4 | - | 3 | 0xxxx | 01101 | |||
| 5 | 1 | 4 | 0xxxxx0 | 0110110 | |||
| 5 | - | - | 0xxxxx1 | - | |||
| 5 | 4 | 1 | 1xxxxx1 | 1001001 | |||
| 5 | 4 | 1 | 1xxxxx | 100100 | |||
| 5 | - | 3 | 1xxxxx | 1101yy | |||
| 5 | 1 | 4 | 0xxxxx | 011011 | |||
| 5 | 3 | - | 0xxxxx | 0010yy | |||
| 6 | 4 | 2 | 0xxxxxx0 | 00100100 | |||
| 6 | - | - | 0xxxxxx1 | - | |||
| 6 | 2 | 4 | 1xxxxxx1 | 11011011 | |||
| 6 | 4 | - | 1xxxxxx | 10010yy | |||
| 6 | - | 4 | 1xxxxxx | 1101101 | |||
| 6 | 4 | - | 0xxxxxx | 0010010 | |||
| 6 | - | 4 | 0xxxxxx | 01101yy | |||
| 7 | - | - | 0xxxxxxx0 | - | |||
| 7 | - | 5 | 0xxxxxxx1 | 11011011 | |||
| 7 | 5 | - | 0xxxxxxx1 | 00100100 | |||
| 7 | - | - | 1xxxxxxx1 | - | |||
| 7 | 2 | 5 | 1xxxxxxx | 11011011 | |||
| 7 | 5 | - | 1xxxxxxx | 10010010 | |||
| 7 | 5 | 2 | 0xxxxxxx | 00100100 | |||
| 7 | - | 5 | 0xxxxxxx | 01101101 | |||
| 8 | 2 | 6 | 0xxxxxxxx0 | 0110110110 | |||
| 8 | - | - | 0xxxxxxxx1 | - | |||
| 8 | 6 | 2 | 1xxxxxxxx1 | 1001001001 | |||
| 8 | 6 | 2 | 1xxxxxxxx | 100100100 | |||
| 8 | - | 5 | 1xxxxxxxx | 1101101yy | |||
| 8 | 5 | - | 0xxxxxxxx | 0010010yy | |||
| 8 | 2 | 6 | 0xxxxxxxx | 011011011 |
yy is either 01 or 10
Table: Sort on patterns
| # of '0' | # of '1' | ||||||
| min | min | P a t t e r n | |||||
| #Blanks | max | max | from | to | |||
| 3 | 2 | 1 | 0xxx0 | 00100 | |||
| 4 | - | - | 0xxxx0 | - | |||
| 5 | 1 | 4 | 0xxxxx0 | 0110110 | |||
| 6 | 4 | 2 | 0xxxxxx0 | 00100100 | |||
| 7 | - | - | 0xxxxxxx0 | - | |||
| 8 | 2 | 6 | 0xxxxxxxx0 | 0110110110 | |||
| 3 | - | - | 0xxx1 | - | |||
| 4 | 3 | 1 | 0xxxx1 | 001001 | |||
| 4 | 1 | 3 | 0xxxx1 | 011011 | |||
| 5 | - | - | 0xxxxx1 | - | |||
| 6 | - | - | 0xxxxxx1 | - | |||
| 7 | - | 5 | 0xxxxxxx1 | 11011011 | |||
| 7 | 5 | - | 0xxxxxxx1 | 00100100 | |||
| 8 | - | - | 0xxxxxxxx1 | - | |||
| 3 | 1 | 2 | 1xxx1 | 11011 | |||
| 4 | - | - | 1xxxx1 | - | |||
| 5 | 4 | 1 | 1xxxxx1 | 1001001 | |||
| 6 | 2 | 4 | 1xxxxxx1 | 11011011 | |||
| 7 | - | - | 1xxxxxxx1 | - | |||
| 8 | 6 | 2 | 1xxxxxxxx1 | 1001001001 | |||
| 3 | 2 | - | 1xxx | 10yy | |||
| 3 | - | 2 | 1xxx | 1101 | |||
| 4 | 1 | 3 | 1xxxx | 11011 | |||
| 4 | 3 | - | 1xxxx | 10010 | |||
| 5 | 4 | 1 | 1xxxxx | 100100 | |||
| 5 | - | 3 | 1xxxxx | 1101yy | |||
| 6 | 4 | - | 1xxxxxx | 10010yy | |||
| 6 | - | 4 | 1xxxxxx | 1101101 | |||
| 7 | 2 | 5 | 1xxxxxxx | 11011011 | |||
| 7 | 5 | - | 1xxxxxxx | 10010010 | |||
| 8 | 6 | 2 | 1xxxxxxxx | 100100100 | |||
| 8 | - | 5 | 1xxxxxxxx | 1101101yy | |||
| 3 | 2 | - | 0xxx | 0010 | |||
| 3 | - | 2 | 0xxx | 01yy | |||
| 4 | 3 | 1 | 0xxxx | 00100 | |||
| 4 | - | 3 | 0xxxx | 01101 | |||
| 5 | 1 | 4 | 0xxxxx | 011011 | |||
| 5 | 3 | - | 0xxxxx | 0010yy | |||
| 6 | 4 | - | 0xxxxxx | 0010010 | |||
| 6 | - | 4 | 0xxxxxx | 01101yy | |||
| 7 | 5 | 2 | 0xxxxxxx | 00100100 | |||
| 7 | - | 5 | 0xxxxxxx | 01101101 | |||
| 8 | 5 | - | 0xxxxxxxx | 0010010yy | |||
| 8 | 2 | 6 | 0xxxxxxxx | 011011011 |
yy is either 01 or 10
I'm searching for more general algorithms. Please contact me.
Updated November 6th, 2013 with general rules for 3 or more blanks (all) and small improvements